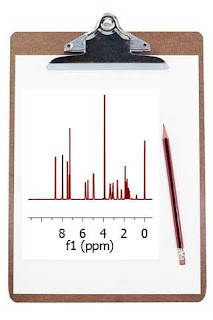
How could this be improved? We could try to extrapolate the FID (somehow) along the columns (F1) to a higher number of points (e.g. 1024). A well known and very simple technique is simply to add zeros, a process called zero-filling, which basically is equivalent to a kind of interpolation in the frequency domain. For example, in this particular case we could try to extrapolate the FID (along t1) from 128 to 1024 points in order to match the number of points along f2. The figure below shows the results:
It can be observed now that the resolution along f1 is slightly higher than in the previous case but we still cannot distinguish the inner structure of the multiplets (e.g. H20a and H23). Zero Filling is certainly a good technique to improve resolution but, of course, it cannot invent new information from where it does not exist. In this case we have zero filled from 128 to 1024 data points (e.g. 4 fold). In theory, zero filling by at least a factor of two is highly recommended because it enforces causality but beyond that, the gain in resolution is purely cosmetic. We might get more data points per hertz, but no new information is achieved as it’s shown in the figure above.
Is there a better way to extrapolate the FID? Yes, and the answer is very evident: L
inear Prediction. In a few words, Forward Linear Prediction uses the information contained in the acquired FID to predict new data points so that we are artificially extending the FID in a more natural way than with Zero Filling. Of course, we cannot create new information with this process but the resulting spectrum will look better. This is illustrated in the next figure:

In this case, we have extended the t1-FID from 128 to 512 data points and then zero-filled up to 1024. Now we can see that the f1-lines are narrower but the couplings cannot be resolved yet.
In recent years there has been great interest in the development of new methods for the time-efficient processing of 2D (nD in general) NMR data. One of the more exciting methods is the so-called
Covariance NMR, a technique developed by
Brüschweiler at al. In fact, there are several types of Covariance NMR: Direct, Indirect Covariance NMR (there is a third method, Unsymmetrical Indirect Covariance which can be considered as a subtype of Indirect Covariance NMR). In this post I will cover only the first type, Direct Covariance NMR leaving, the other 2 types for future posts.
Before going any further with Covariance NMR, let’s see the results of applying this technique to the same spectrum. This is what we get:

At first glance, this result looks like a kind of magic: Now the splitting corresponding to H20a and H23 are clearly resolved in both dimensions. Actually, the resolution along F1 is virtually analogous to that of the F2 dimension. How did we arrive to such a good result? From an intuitive stand point, what we have attained here was a transfer of the resolution of F2 to the F1 dimension. In other words, we have applied a mathematical process which takes advantage of the higher spectral resolution in the F2 dimension to transfer it to the F1 one.
Mathematically, direct Covariance NMR is extremely straightforward as defined by the following equation:
C = (F'F) (1)
Where C is the symmetric covariance matrix, F is the real part of the regular 2D FT spectrum and F' its transpose (NOTE: direct covariance NMR can also be applied in the mixed frequency-time domain, i.e., when the spectrum has been transformed along F2. In this case, a second FT will not be required – nor apodization nor phase correction along the indirect dimension).
In order to approximate the intensities of the covariance spectrum to those of the idealized 2D FT spectrum, the square root of C should be taken. Root squaring may also suppress false correlations which may be present in F'F due to resonance overlaps. Taking the square root of C matrix is in practice done using standard linear algebra methods (in short, diagonalizing the matrix and then reconstructing C^(1/2) using eigenvectors and the square roots of eigenvalues).
So direct Covariance NMR allows us to produce a 2D spectrum in which the resolution in both dimensions is determined by the resolution of the spectrum along the direct dimension. I have created a stacked plot representation with the 1D projections obtained from the different processing methods described in this post (Zero-Filling, Linear Prediction and Direct Covariance NMR). I think that this plot shows the power of the Covariance NMR method.

There is nothing magic about Covariance NMR. It’s a process with a strong mathematical background based on the well-known
Parserval’s theorem. An elaborate discussion of this method is beyond the scope of this post (at least for the time being), but it has been nicely described in the following articles by Brüschweiler et al.
[1] R. Bruschweiler and F. Zhang, J. Chem. Phys., 120, 5253 (2004)
[2] F. Zhang and R. Bruschweiler, Chem Phys Chem, 5, 794 (2004)
[3] R Bruschweiler, J. Chem Phys., 121, 409 (2004).
[4] N. Trbovic, S. Smirnov, F. Zhang, and R. Bruschweiler, J. Magn Reson, 171, 277 (2004).
[5] F. Zhang, N. Trbovic, J Wang, and R. Bruschweiler, J. Magn. Reson., 174, 219, 2005).
[6] Y CHen, F. Zhang, W. Bermel and R Bruschweiler, JACS, 128, 15564 (2006)
[7] F Zhang and R Bruschweiler, Angew Chem., Intl. Ed., Engl., 46, 2639 (2007)
[8] Y. Chen, F. Zhang, D. Snyder, Z Gan, L. Bruschweiler-Li, and R. Bruschweiler, J. Biomol. NMR, 38, 73 (2007)
If you still feel skeptical about Covariance NMR, just try it out. We have recently implemented this technique in Mnova. This version is still in alpha stage but if you want to try it, just send me an email (my email is carlos followed by ‘at’ and mestrelab.com) and I will give you a link to download this alpha version of Mnova.
BTW, I’m proud to say that MestReC was the first NMR software package (apart from the in-house algorithms developed by Brüschweiler group) which offered Covariance NMR processing (here is the
proof). Now we have ported and greatly enhanced MestReC old implementation in
Mnova. Now Covariance NMR is not only much faster than it was in MestReC; it’s also easier to use and more versatile. I hope you will enjoy it!.
Before I finish, I’d like to acknowledge Dr. Fengli Zhang for his support while implementing Covariance NMR into MestReC.